2024欧洲杯(China·认证)下单平台-Royal Club

RMS是什么

RMS即真有效值，是对交流信号幅度的基本量度，可以分别从实用角度和数学角度予以定义。

从实用角度定义是：一个交流信号的真有效值等于在同一电阻性负载上产生同等热量所需的直流量。例如，1V真有效值交流信号与1V直流信号在同一电阻上产生的热量相同。

从数学角度定义是：真有效值定义如下：

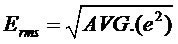
真有效值等同于零平均值统计信号的标准偏差。这包括求信号的平方，取平均值，然后获得其平方根。取平均的时间和信号的特性相关，对于周期信号，则使用完整周期进行平均即可，但是对于非周期信号，取平均值的时间必须足够长，以便能在所需的近似最低工作频率进行滤波。

按照RMS的定义，一个交流信号的RMS值等于在同一电阻性负载上产生同等热量所需的直流量。所以真有效值是从热量角度定义的，根据热量的定义，有以下公式：

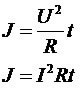
所以根据RMS定义，有以下公式：

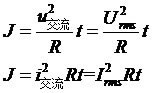
消去R值，可以得到

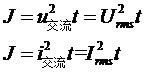
两个等式的模型一样，等效为一个等式：

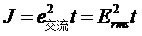
交流信号的幅度值是时刻变化的，但是我们将时间t细分为Δt，由于Δt很小，可以认为在Δt时间内交流信号的幅度值不变化，值为e(i)，并且热量是可以累积的，所以有：

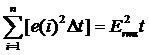
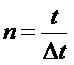
所以有：

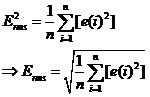
推导得到真有效值的数学定义，等效于对被测信号的实时采样值进行平方和后求平均，然后开方。求平均是一个将变化信号趋于稳定的运算，对于周期信号，因为其周期变化，所以只要对其完整周期进行评价，其结果就是一个稳定值，所以平均的时间t可以取周期信号的n个完整周期T。对于非周期信号，由于其变化没有规律，所以只能在保证测量结果输出的前提条件下，尽可能长时间的进行平均。

对于周期信号，当Δt无穷小时，我们可以得到RMS值得积分表达形式：

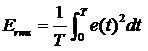
理论上，热转换是最简单、最直接的方法，但实际上，它却是最难以实现、成本最高的方法。这种方法涉及到将未知交流信号的热值与已知的校准直流基准电压的热值进行比较，测量框图如图1所示。基准电阻R2和信号电阻R1的等效参数模型必须是近似完全一致，并且近似纯电阻性。S1和S2是两个性能完全一样的热电转换器件，将R1和R2产生的热量转换为电形式，热隔离带用来阻断R1和R2之间的热传递，所以最终A2会调整一个直流输出值，使基准电阻R2与信号电阻R1之间的温差为零，此时这两个匹配电阻的功耗完全相同。因此，根据真有效值的基本定义，直流基准电压值将等于未知信号电压的真有效值。

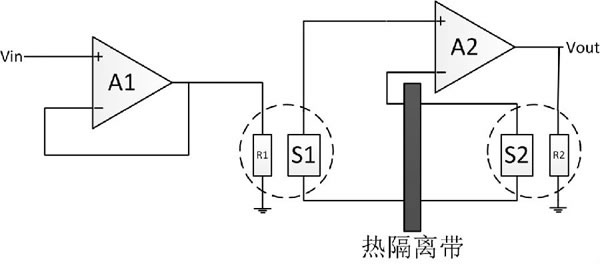
模型非常简单，也非常好理解，但是每个热单元都必须含有一个稳定的、低温度系数电阻R1和R2，电阻与线性温度电压转换器S1和S2发生热接触，并且要保证热传递性能一致。